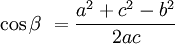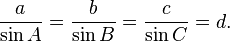Hukum cosinus
Hukum kosinus, atau disebut juga
aturan kosinus, dalam
trigonometri adalah aturan yang memberikan hubungan yang berlaku dalam suatu
segitiga, yaitu antara panjang sisi-sisi segitiga dan
kosinus dari salah satu
sudut dalam segitiga tersebut.
Perhatikan gambar segitiga di kanan.
Aturan kosinus menyatakan bahwa

dengan

adalah sudut yang dibentuk oleh sisi
a dan sisi
b, dan
c adalah sisi yang berhadapan dengan sudut

.
Aturan yang sama berlaku pula untuk sisi
a dan
b:


Dengan kata lain, bila panjang
dua sisi sebuah segitiga dan sudut yang diapit oleh kedua sisi
tersebut diketahui, maka kita dapat menentukan panjang sisi yang
satunya. Sebaliknya, jika panjang dari tiga sisi diketahui, kita dapat
menentukan besar sudut dalam segitiga tersebut. Dengan mengubah sedikit
aturan kosinus tadi, kita peroleh:

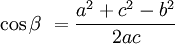

Hukum Kosinus Pertama



Hukum Kosinus Kedua



Hukum sinus
Dalam trigonometri, hukum sinus ialah pernyataan tentang segitiga yang berubah-ubah di udara. Jika sisi segitiga ialah (kasus sederhana) a, b dan c dan sudut yang berhadapan bersisi (huruf besar) A, B and C, hukum sinus menyatakan
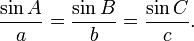
Rumus ini berguna menghitung sisi yang tersisa dari segitiga jika 2 sudut dan 1 sisinya diketahui, masalah umum dalam teknik
triangulasi.
Dapat juga digunakan saat 2 sisi dan 1 dari sudut yang tak dilampirkan
diketahui; dalam kasus ini, rumus ini dapat memberikan 2 nilai penting
untuk sudut yang dilampirkan. Saat ini terjadi, sering hanya 1 hasil
akan menyebabkan seluruh sudut kurang daripada 180°; dalam kasus lain,
ada 2 penyelesaian valid pada segitiga.
Timbal balik bilangan yang yang digambarkan dengan hukum sinus (yakni
a/sin(
A)) sama dengan
diameter d . Kemudian hukum ini dapat dituliskan
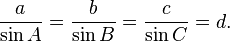
Dapat ditunjukkan bahwa:
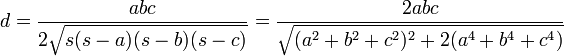
di mana
- s merupakan semi-perimeter

Turunan
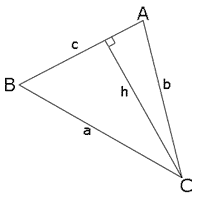
Buatlah segitiga dengan sisi
a,
b, dan
c, dan sudut yang berlawanan
A,
B, dan
C. Buatlah garis dari sudut
C pada sisi lawannya
c yang menonjol sekali dalam 2 segitiga siku-siku, dan sebut panjang garis ini
h.
Dapat diamati bahwa:
 and
and 
Kemudian:

dan

Melakukan hal yang sama dengan garis yang digambarkan antara sudut
A dan sisi
a akan menghasilkan:

 adalah sudut yang dibentuk oleh sisi a dan sisi b, dan c adalah sisi yang berhadapan dengan sudut
adalah sudut yang dibentuk oleh sisi a dan sisi b, dan c adalah sisi yang berhadapan dengan sudut  .
.
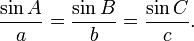
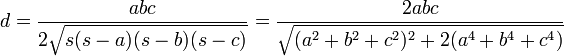

 and
and